本文源自汇编课上的一个问题:8位二进制数的原码能表示什么范围的数?大家知道8位二进制数应该可以表示
2^8=256个数,可是原码的第1位表示正负,不算0 剩下7位可以表示2^7-1=127个数,再算上0,一共是2*(2^7-1)+1=255个数,所以到底漏了谁?
我们知道计算机最初就是为了完成计算而设计制造的,那么数字1在计算机中是怎样表示的呢?
二进制
由于电路最容易表示的是高低电平(高: 1 ;低: 0 ),而我们知道数在不同进制下虽然表示不同,但是可以一一对应,即进制之间是相互等价的。所以自然,二进制成了不二之选。
但是负数又该怎么办呢?
负数
数字的正负只是记号,可以用0、1表示。于是,原码诞生了。
数字变为二进制编码的原初转换即为原码。转换规则如下:
-
非负数
直接转换为二进制
-
负数
先将绝对值转换为二进制,再将最高位写1,表示负数
以8位(8 bit)二进制数为例, 10 的原码是 00001010 , -3 的原码是 10000011 。那么一个很自然的问题是:8位二进制数能表示什么范围的有符号数2呢?
如果不考虑负数,我们知道8位二进制数可以表示 0~255 ( 2^8=256 个数);考虑负数后,第1位表示正负是两种可能,后面7位去除 0000000 的情况是 2^7-1=127种可能(保证严格正负,即这些情况是不重复的),最后还剩 00000000 、 10000000 这两种情况( 2*(2^7-1)+2=2^8 ),那这两个数对应的十进制数究竟是什么呢?除去这两个数,现在已经表示的数是 -1~-127 和 1~127 ,0还没有表示,哪个表示0呢,另一个又表示哪个数字呢?我们不妨将这些确定的数先简单列出来。
| 十进制 | 二进制 | | | 十进制 | 二进制 |
|---|---|---|---|---|
| 1 | 00000001 | | | -1 | 10000001 |
| 2 | 00000010 | | | -2 | 10000010 |
| 3 | 00000011 | | | -3 | 10000011 |
| … | … | | | … | … |
| 126 | 01111110 | | | -126 | 11111110 |
| 127 | 01111111 | | | -127 | 11111111 |
其实根据先前的定义,0的原码就是 00000000 ,可为什么会有这个定义呢? 10000000 表示的又是哪个数字?此外,虽然可以使用上面的原码表示负数,但是方便计算机进行运算吗?我们知道计算机最擅长的是做加法运算,如果负数以一种恰当的方式被表示,那么 a-b 就可以看作 a+(-b) ,从而将减法转换为加法。原码可以做到吗?
观察上表就会发现负数的二进制表示随着数的不断变小,反而在增加,如 -1>-127 ,而 10000001<11111111 ,这样是不可能将减法转换为加法的(正负求和规律与正正求和、负负求和不一致),例如 1+(-1) 与 2+(-2) 对应的二进制相加是 00000001+10000001 和 00000010+10000010 ,结果分别为 10000010 和 10000100 ,显然这两个二进制结果不相等,而从十进制看结果应该均为0,矛盾。所以原码实际上并没有解决负数在计算机中的表示问题。
不过,它的思路是正确的,可以用0、1表示正负。
补码
在引入补码前,我们先看一个相关的例子。
现在有一个时钟(1点到12点),如果认为12点是0点,那么3点就是 +3 ,表示时间向后过了3个小时,11点就是 +11 ,表示时间向后过了11个小时,那 -2 是不是表示时间向前了2小时呢,所以可以认为 -2 表示的是10点吗?
| 时钟 | 数字 | 数字 |
|---|---|---|
| 12点 | 0 | 0 |
| 1点 | 1 | -11 |
| 2点 | 2 | -10 |
| … | … | … |
| 10点 | 10 | -2 |
| 11点 | 11 | -1 |
所以某种程度上 -2=10 ?
原因是时钟以 12 为周期,一个数放在这周期里就相当于 mod 12 (除以12取余数),变成了余数。而 -2 与 10 在 mod 12 的情况下,表示的含义是一样的。再进一步,可以认为 12 就是时钟能表示的最大信息量。
那么,计算机中的负数是否可以按照同样的思路表达?
例如,在8位二进制下,如何表示 -1 ?
首先,8位二进制,相当于 mod 2^8=256 (加上 256 或者减去 256 对这个数没有影响,因为 256 超过可表达的范围无法记录),所以我们给 -1 加上 256 试试,则 -1+256=255 的二进制将表示 -1 。 255 本身不在有符号数的表示范围内,所以不会产生误解。如果我们继续下去并考虑正数的情况(正数直接转二进制),可以得到这样一张十进制与二进制映射表。
| 十进制 | 二进制 | 十进制 | 二进制 | |
|---|---|---|---|---|
| 1 | 00000001 | -127 | 10000001 | |
| 2 | 00000010 | -126 | 10000010 | |
| 3 | 00000011 | -125 | 10000011 | |
| … | … | … | … | … |
| 126 | 01111110 | -2 | 11111110 | |
| 127 | 01111111 | -1 | 11111111 |
从 -127 开始到 -1 ,再从 1 到 127 ,数字不断变大;再看对应的二进制, -127 ( 10000001 )到 -1 ( 11111111 )也是不断变大, 1 ( 00000001 )到 127 ( 01111111 )也是不断变大;可是 -1 ( 11111111 )到 1 ( 00000001 )似乎变小了。没关系,我们先来确定 -1 和 1 之间的 0 的二进制表示是什么。如果我们给 1 ( 00000001 )减1,得到 0 的二进制表示是 00000000 ;给 -1 ( 11111111 )加1,得到 0 ( 100000000 ),舍弃第9位的1后变为 00000000 (8位二进制只能记录8位数字)。所以可以确定 0 的二进制就是 00000000 ,而不是 10000000 ,那么 10000000 是哪个数的二进制呢?
从上表看就很容易知道了, -1 ( 11111111 )到 -127 ( 10000001 )在不断减小,继续减小 1 是 -128 ( 10000000 ),此时 2^8=256 个8位二进制全部对应上了十进制数。这样的二进制,我们称为补码。
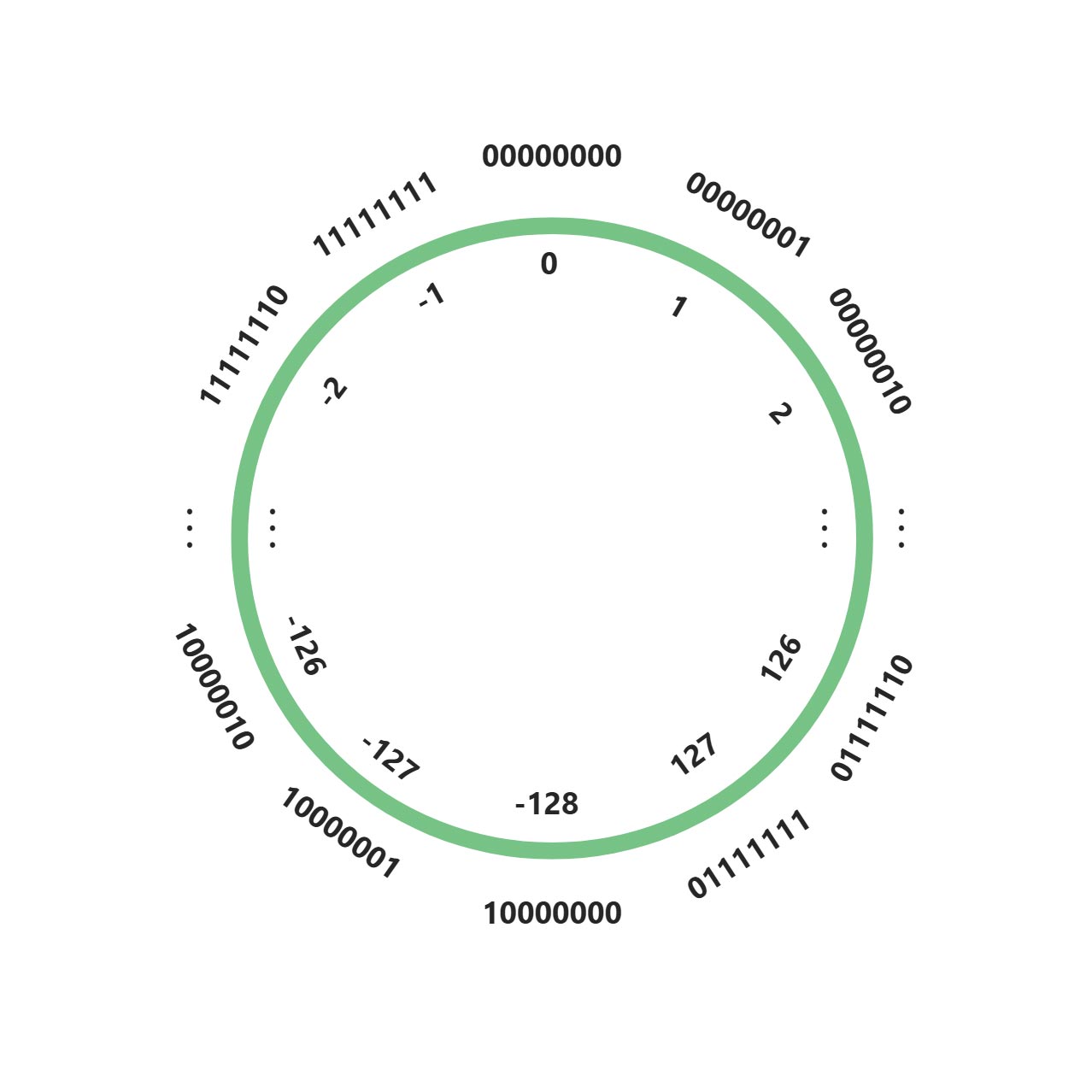
上图清晰地表示了十进制与对应的补码的映射关系,所以明显地,8位二进制数能表示的有符号数(要求对称的情况下)是 -128~127 。理论上,我们其实可以给每个数加上或减去一个数做偏移,使得8位二进制数能表示的有符号数是 -127~128 、 -60~195 或者 -1~254 等,但是显然没有补码的表示方法好(非负直接转换为二进制;负数加 256 再转换为二进制)
比较原码和补码,回头看原码之所以不能作为计算机表示负数的方法,正是它的二进制表示不是递增加一(原本的十进制数 -127 到 127 是递增加一的),所以转换后不满足加法运算规律;而补码是满足递增加一的。
算法
前面补码的计算过程中有一步是给原数(负值)加上对应位数的一个数(如 8 bit就是 2^8 ),这里存在一个严重的问题。我们计算补码就是为了表示负数,将减法运算转换为加法运算,但是依据上面的算法,计算补码的过程中就需要做减法运算,所以 ![]()
那有没有其他算法可以将一个十进制数转换为补码呢?
| 十进制 | 原码 | 补码 |
|---|---|---|
| -1 | 10000001 | 11111111 |
| -2 | 10000010 | 11111110 |
| -3 | 10000011 | 11111101 |
| … | … | … |
| -126 | 11111110 | 10000010 |
| -127 | 11111111 | 10000001 |
由于计算十进制数的原码是不难的,负数只需要先将绝对值转换为二进制,再将最高位写1,所以列出 -1 到 -127 的原码和补码,试图找到原码转换为补码的方法。经过观察不难发现,原码和补码就像是颠倒了一样,一个从 10000001 到 11111111 ,另一个从 11111111 到 10000001 ;还有就是原码和补码的最高位均为1。所以很自然会去尝试在保证最高位不变的情况下,将其余位做变反处理( 0 变 1 ; 1 变 0 ),而这就是反码(负数的反码;正数的反码和原码相同)。
| 十进制 | 原码 | 反码 | 补码 |
|---|---|---|---|
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| … | … | … | … |
| -126 | 11111110 | 10000001 | 10000010 |
| -127 | 11111111 | 10000000 | 10000001 |
观察上表不难发现,反码加1就是补码。至此,已经找到计算负数的补码的方法了。可是还有一个问题我们还没有解决:原码为 10000000 的十进制数是多少?
让我们倒着推导一下! -128 的补码是 10000000 ,反码等于补码减1,是 11111111 (借位,且负数的原、反、补第一位都是1;非负数的第一位都是0),原码是反码除第一位全部变反,是 10000000 !所以原码为 10000000 的十进制数是 -128 !
总结
| 十进制 | 原码 | 反码 | 补码 |
|---|---|---|---|
| 127 | 01111111 | 01111111 | 01111111 |
| 126 | 01111110 | 01111110 | 01111110 |
| … | … | … | … |
| 3 | 00000011 | 00000011 | 00000011 |
| 2 | 00000010 | 00000010 | 00000010 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| … | … | … | … |
| -126 | 11111110 | 10000001 | 10000010 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | 10000000 | 11111111 | 10000000 |
原码、反码、补码的引入是为了解决计算机中使用二进制表示负数的问题,先是从0、1表示正负的思路开始,到通过加除数( mod )计算补码,最后是加入了反码找到一种计算补码的通用算法。由此,也就容易理解为什么非负数的原码、反码、补码都相同,都是直接转换为二进制。
最后附上依据上面的算法用C写的计算十进制数补码的程序(8 bit),点击 ![]() 这里下载
这里下载
Leave a comment